

The second method is by using the properties of logs to write ln(2x) into a form which differentiable without needing to use the chain rule.
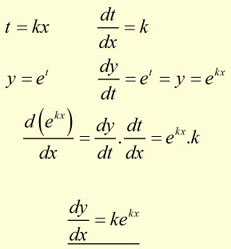
The first method is by using the chain rule for derivatives. There are two methods that can be used for calculating the derivative of ln(2x). (Just simply apply the power rule to each term in the function separately).How to calculate the derivative of ln(2x) Note that the sum and difference rule states:
dx Also, remember that the derivatives of a constant is zero: d ( c ) = 0. If n is any real number, then d (x n ) = nx n-1. Which is a lengthy procedure used to evaluate the derivative of a function. Thankfully, easier methods have been developed to help evaluate derivatives more quickly. Understanding the Derivativeĭifferentiation is a method to compute the rate at which a dependent variable y changes with respect to the change in the independent variable x. This rate of change is called the derivative of y with respect to x. There are many different notations to denote “take the derivative of.” The relationship between y and x is usually denoted by f(x) and its derivative is usually denoted as f‘(x) or y’ or dy/dx. The definition of the derivative is given by: In calculus, a derivative can be thought of as an instantaneous rate of change that is, how much a quantity is changing at a given point. Let’s take a closer look at how we can differentiate a function easily by the use of some helpful rules.
#Derivative of log rules manual

#Derivative of log rules how to
How to Find Articles Using Google Scholar.How to Find Books on the Library Website.Introduction to Trigonometric Functions.Avoiding Common Math Mistakes in Trigonometry.Transformations of Trigonometric Functions.Transformations of Exponential and Logarithmic Functions.Transformations and Graphs of Functions.Least Squares Trendline and Correlation.Domain and Range of Trigonometric Functions.Domain and Range Exponential and Logarithmic Fuctions.Applications Involving Exponential Models.Solving Exponential and Logarithmic Equations.Transformation of Exponential and Logarithmic Functions.Domain and Range of Exponential and Logarithmic Functions.Exponential and Logarithmic Functions: Basics.More in Basic Math Skills and Number Sense.Avoiding Common Math Mistakes-Working with negatives.Avoiding Common Math Mistakes-Square Roots.Avoiding Common Math Mistakes-Simplifiying.Avoiding Common Math Mistakes-Trigonometry.Avoiding Common Math Mistakes-Expanding.Learn more about Indigenous Education and Cultural Services Our past defines our present, but if we move forward as friends and allies, then it does not have to define our future. We all have a shared history to reflect on, and each of us is affected by this history in different ways. This history is something we are all affected by because we are all treaty people in Canada. Most importantly, we acknowledge that the history of these lands has been tainted by poor treatment and a lack of friendship with the First Nations who call them home. We acknowledge this land out of respect for the Indigenous nations who have cared for Turtle Island, also called North America, from before the arrival of settler peoples until this day. These lands remain home to many Indigenous nations and peoples. The lands we are situated on are covered by the Williams Treaties and are the traditional territory of the Mississaugas, a branch of the greater Anishinaabeg Nation, including Algonquin, Ojibway, Odawa and Pottawatomi. We are thankful to be welcome on these lands in friendship.


 0 kommentar(er)
0 kommentar(er)
